2018년 11월 26일
허프만 코드 (Huffman Code)
1. 문자의 빈도 기반 접두부호 생성, 허프만 코드의 개요
(1) 허프만 코드의 개념
- 무손실 압축 위한 엔트로피 부호화로, 데이터 등장 빈도에 따라 다른 길이 부호 사용 알고리즘
| 개념도 | 설명 |
|---|---|
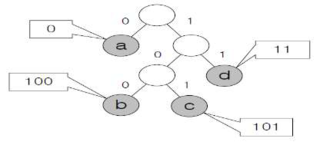 | – 접두어 코드 사용 압축 – 접두어 코드 표현 왼쪽 서브 노드: 0 오른쪽 서브 노드: 1 – 루트→리프 경로가 접두어 |
- 허프만 코드는 무손실 압축, 심볼의 출현 빈도에 따른 가변 길드 코드와 접두사 코드 생성
2. 허프만 코드의 수행 알고리즘
- 압축: 만들어진 이진 트리 기반 해당 문자 접두어 코드로 변환
- 해제: 노드 탐색 시 리프 노드까지 트리의 좌, 우 노드 순회
| 구분 | 수행 절차 | 설명 |
|---|---|---|
| 압축 | 초기화 | – 모든 문자 출현 빈도에 따라 나열 |
| 해 선택 | – 빈도수 가장 낮은 두 개 결합 – 두 노드 위 부모 노드 생성, 연결 | |
| 실행가능성 검사 | – 기호를 가진 노드가 리프 노드 조건 만족하는지 여부 검사 | |
| 최종 해 검사 | – 허프만 트리 완성 여부 – 미완성 시 2, 3단계 반복 수행 | |
| 해제 | 버퍼 준비 | – 허프만 트리와 압축 해제된 데이터를 담을 버퍼를 준비 |
| 비트 해석 | – 압축 데이터에 미탐색 부분 Read | |
| 트리 순회 | – Read 비트가 0 → 왼쪽 노드로 이동 – Read 비트가 1 → 오른쪽 노드로 이동 |
3. 허프만 코드를 이용한 압축과 복호화 과정
(1) 허프만 코드를 이용한 압축 과정 (사례: aaabaacdd)
| 절차 | 허프만 트리 생성 | 설명 |
|---|---|---|
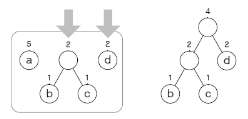
| 초기화 | – aaabaacdd의 빈도 a:5, b:1, c:1, d:2 | |
| 해 선택 | 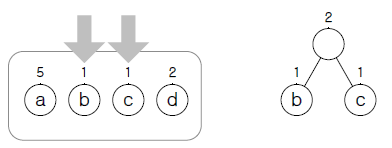 – b, c 이용 트리 생성 | – 현재 시점에서 빈도가 가장 작은 노드 두 개 선택 (리프 노드 조건) |
| 실행 가능성 검사 | – 기호 가진 노드가 리프 노드 조건을 만족하는지 검사 | |
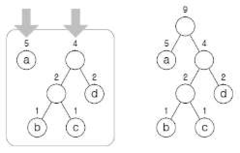
| 최종해 검사 | – 모든 노드가 트리에 속하도록 완성까지 반복 수행, 검증 (완성도 개념도 참조) |
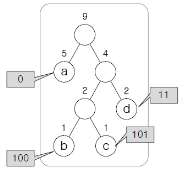
- 압축 결과: 0 0 0 100 0 0 101 11 11
| a | a | a | b | a | a | c | d | d |
| 0 | 0 | 0 | 100 | 0 | 0 | 101 | 11 | 11 |
- 원본 데이터(ASCII 코드 시)의 크기는 72bit → 15bit로 압축
(2) 허프만 코드를 이용한 복호화 과정
| 절차 | 허프만 트리 | 버퍼 상황 |
|---|---|---|
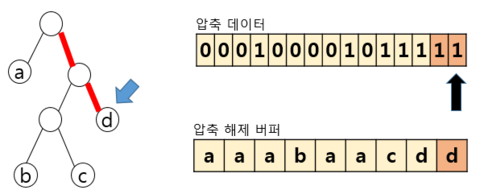
| 버퍼 준비 | 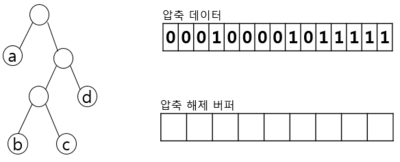 – 허프만 트리, 압축 데이터와 버퍼(루트 숫자) 준비 | |
| 비트 해석 및 트리 해석 | 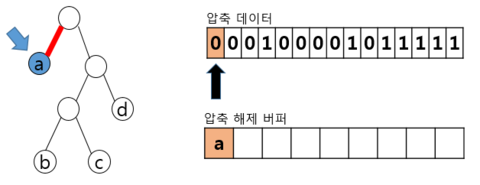 – 압축 해제된 버퍼 Read – 왼쪽으로 이동, 해당하는 리프 노드의 a를 압축 해제 버퍼에 추가하고 루트노드로 복귀 – 세 번째 비트까지 0 계속 Read, 3번째까지 a 추가 | |
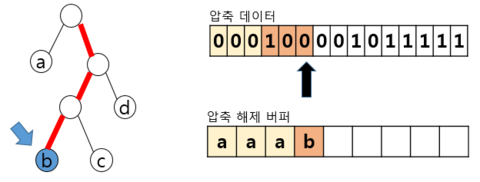 – 1 해당, 오른쪽 이동, 리프 노드X → 다음비트 Read – 0 해당, 왼쪽 이동, 리프 노드X → 다음비트 Read – 0 해당, 왼쪽 이동, 리프 노드 b를 압축 해제 버퍼 에 추가, 루트 노드로 복귀 | ||
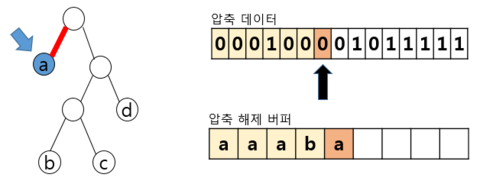 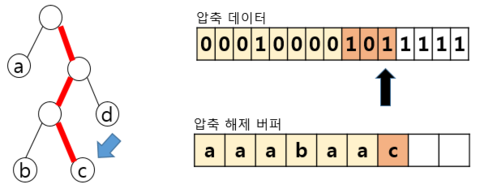 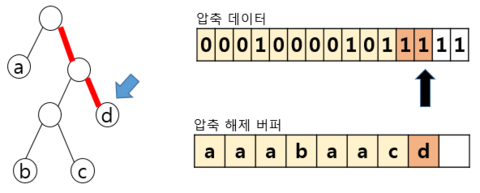
– 압축 데이터에 해당하는 전체 대상을 수행시 까지 반복 수행 후 종료 | ||
4. 허프만 코드 알고리즘 코드
code = 0 while more symbols: print symbol, code code = (code + 1) << ((bit length of the next symbol) – (current bit length)) |
2 Comments
왼쪽이 빈도수가 낮아야 하고, 오른쪽이 빈도수가 높아야하는거 아닌가요?
허프만 코드 트리 생성 시 반드시 출현 빈도 수가 낮은 문자는 왼쪽, 출현 빈도 수가 높은 문자는 오른쪽으로 구분할 필요는 없습니다. 중요한 것은 문자 출현 빈도에 따라 낮은 빈도에서 높은 빈도의 문자 순서로 리프 노드로 구성된 트리를 생성하는 것이고, 생성된 트리로 만들어진 접두어 코드를 문자에 정확히 적용하고 해석하는 것입니다. 제가 잘못 알고 있을 수도 있으니 혹시 잘못된 점이 있다면 말씀 부탁드려요^^