2018년 12월 11일
CPM (Critical Path Method)
1. 프로젝트 일정관리 CPM의 개요
(1) CPM(Critical Path Method)의 개념
- 프로젝트 납기일에 영향을 미치는 Activity 집합으로, 프로젝트의 시작과 끝을 나타내는 노드(node) 간을 연결하는 화살표 모양의 Activity로 구성한 프로젝트 일정관리 기법
(2) CPM의 특징
- 프로젝트의 최소기간을 결정하는 데 사용되는 일정 네트워크 분석기법
- 프로젝트에서 중점적으로 관리해야 하는 작업의 경로
2. CPM를 활용한 수행기간 추정
(1) CPM 절차
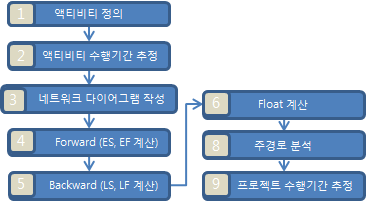
| 용어 | 설명 |
|---|---|
| ES(Early Start) | 어떤 활동이 가장 빨리 시작할 수 있는 날 |
| EF(Early Finish) | 어떤 활동이 가장 빨리 끝날 수 있는 날 |
| LS(Late Start) | 종료일에 영향이 없으며, 가장 늦게 시작해도 되는 날 |
| LF(Late Finish) | 종료일에 영향이 없으며, 가장 늦게 종료할 수 있는 날 |
| 총 여유 (Total Float) | 종료일에 영향이 없으며, 지연될 수 있는 여유 시간 |
| 자료 여유 (Free Float) | 다음 활동의 초기 시작에 영향이 없으며, 지연될 수 있는 활동의 여유 시간 |
| 전진계산 (Forward) | 시작일을 기준으로 작업의 기간, 연관관계를 통해 예상 종료일을 도출해 내는 방식(ES, EF) |
| 후진계산 (Backward) | 종료일을 기준으로 작업의 기간, 연관관계를 통해 예상 시작일을 도출해 내는 방식(LS, LF) |
(2) 주경로 도출 방법 – 일자방식
| (활동정의) 작업 | (활동기간 산정) 기간(일 (Duration)) | (활동순서 배열) 선행작업 |
|---|---|---|
| A | 3d | – |
| B | 2d | A |
| C | 2d | B, D |
| D | 4d | A |
| E | 6d | D |
| F | 3d | C, E |
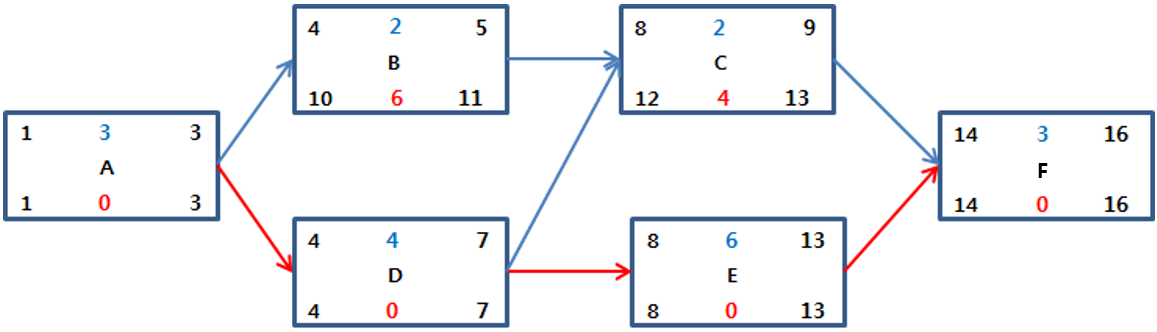
– Forward Scheduling
ES와 EF를 계산: EF = ES + 기간 – 1, 다음 ES = 선행 EF + 1
– Backward Scheduling
LS와 LF를 계산: LF = 후행 LS – 1, LS = LF – 기간 + 1
– Float 계산 및 주 경로 분석
Float = LF – EF or LS – ES
주 경로(Critical Path)는 Float이 “0”인 활동을 연결한 경로(A-D-E-F)
| Free Float | Total Float |
|---|---|
| 후행활동의 ES를 지연 시키지 않으면서 가질 수 있는 여유기간 | 종료일을 지연시키지 않고 활동이 가질 수 있는 총 여유 시간 |
| B: 2d, C: 4d, 나머지: 0d | B: 6d, C: 4d, 나머지 0d |
3. CPM의 한계 극복
- 다중경로의 영향(Multi-path effects, path convergence)으로 프로젝트가 지연될 리스크가 증가됨을 반영 하지 못함
- PERT와 CPM의 장점을 도입하여 병행적용함으로 일정추정과 단축 가능
- 일정 계획 시 자원이 무한하다고 가정하여 제약이론 도입 및 주기적 CPM 계산의 요구를 해결하기 위해 자동화 도구가 필요
5 Comments
B의 활동의 기간이 이상한듯 하네요 4가 아니고 2인듯합니다
이해쉽게 설명 해주셔서 감사합니다
잘못된 부분 지적 감사드리며, 진행도 그림 수정하였습니다. 도움이 되셨다니 다행입니다.^^
자료 정리가 엄청 잘 되어있네요. 도움 많이 됐어요 감사합니다!
CPM예제 풀이에서 제일 오른쪽 네모 네이밍(A->F) 수정 필요 한 것 같습니다. 내용 공유 많은 참고 되었습니다. 감사합니다.
본문 그림 수정하였습니다. 잘못된 부분 알려주셔서 감사합니다!