2019년 2월 19일
McCabe 회전 복잡도
I. 코드 품질의 정량적 측정, McCabe 회전 복잡도
| 개념 | 소스코드 복잡도의 정량적 표현을 위해 제어 흐름을 그래프로 표현하는 측정 지표 | |
|---|---|---|
| 특징 | 정량 지표 | 소스코드 복잡도를 정량적 측정/평가 |
| 구조적평가 | SW산출물 실제 동작전 상태 품질 측정 | |
| 간접 방식 | 효율, 기능성, 품질 등 간접적 측정 | |
- 코드 복잡도 계산 위해 그래프 표현 및 계산식 존재
II. McCabe 회전 복잡도 측정 기법 및 복잡도 평가 지표
가. McCabe 회전 복잡도 측정 기법
| 구분 | 측정 기법 | 설명 |
|---|---|---|
| 계산식 | V(G)=E-N+2 | – 노드 수(N) 및 간선 수(E)계산 |
| V(G)=P+1 | – 조건 분기문(P) 수로 계산 | |
| 그래프 구성 |  | – Node – 프로세싱 태스크 표현 |
| – Edge – 태스크 간 제어 흐름 표현 | ||
| 그래프 표현 | – Sequence – 분기, 반복 없는 태스크 | |
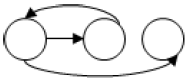 | – While – 사전 조건에 의한 반복 제어 | |
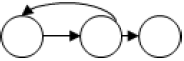 | – Until – 사후 조건에 의한 반복 제어 | |
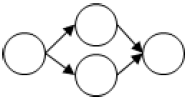 | – If – Else – 조건 분기문에 의한 제어흐름 |
나. McCabe 평가 지표
| 지표 | 평가 기준 | 설명 |
|---|---|---|
| 복잡도 1 ~ 10 | – 구조적 – 안정된 코드 | – 높은 테스트 가능성 – 낮은 위험도 및 비용 |
| 복잡도 11 ~ 20 | – 다소 복잡 | – 중간 수준 테스트 가능성 – 중간 수준 위험도 및 비용 |
| 복잡도 21 ~ 50 | – 매우 복잡 | – 낮은 테스트 가능성 – 높은 위험도 및 비용 |
| 복잡도 40이상 | – 테스트 불가 | – 매우 높은 위험 및 비용 |
- ISO26262, MISRA에서 SW안전성 위해 복잡도 측정 요구
III. McCabe 회전 복잡도 계산예제
가. 문제 그래프 식 표현
| 노드 | 구문 |
|---|---|
| int x = 0; int a[] = {1, 2, 3, 4, 5}; | |
| 1 | while(x < 5) |
| 2 | switch(a[x] % 2) { |
| case 0: | |
| 3 | printf(“a[%d] is even\n”, x); |
| break; | |
| case 1: | |
| 4 | printf(“a[%d] is odd\n”, x); |
| break; | |
| default: | |
| 5 | printf(“Fault result: a[%d]\n”, x) |
| } | |
| 6 | x++; |
| } | |
| 7 | printf(“Program terminated.\n”); |
- 그래프
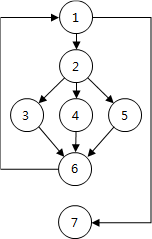 |
나. McCabe 회전 복잡도 계산
| 구분 | 설명 |
|---|---|
| V(G)=E-N+2 | – 총 간선 수 (E): 9, 총 노드 수 (N): 7 – 회전 복잡도 V(G) = 9 – 7 + 2 = 4 |
| V(G)=P+1 | – 총 조건 분기문 (P) = 3 (if-then, case 조건 수, 단 else, default는 제외) – 회전 복잡도 V(G) = 3 + 1 = 4 |
| 회전 복잡도 | 주어진 문제의 회전 복잡도는 4 |
- 기존 McCabe 계산 단점 보완한 Modified, Strict Cyclomatic Complexity를 이용하여 복잡도 측정 가능