2018년 12월 5일
나이브 베이지안 (Naive Bayesian)
I. 나이브 베이지안 개념
문서나 데이터 요소 등장 확률 도출을 위해 베이즈 정리 기반 독립적 확률 벡터 분류 기법
II. 나이브 베이지안 분류기 수행 절차
가. 나이브 베이지안 분류 기법 수행 절차
| 절차 | 설명 | 수식 |
|---|---|---|
| 지도 학습 분류 | – 분류기 실행 전 학습 벡터 결과 기반 분류 수행 | C = {Comedy, Action} |
| 입력 벡터 선택 | – 분류 요소로 이루어진 벡터 | D = e1, e2, e3, …, en |
| 조건부확률 계산 | – 입력 벡터가 속한 클래스 결정 | P(C1|D) = P(C1|e1, e2, …, en) |
| 확률 계산 | – 클래스 별 분류 확률 계산 | P(C1|D) = (P(D|C1)P(C1))/P(D) |
| 클래스선택 | – 최대 확률에 해당하는 클래스 선택 | |
나. 나이브 베이지안 분류 기법 적용 사례
| – “대출” 단어 존재 시 스팸 확률 | P(스팸|대출) = (P(대출|스팸)P(스팸))/P(대출) |
| – “대출” 단어 존재 시 스팸이 아닐 확률 | P(정상|대출) = (P(대출|정상)P(정상))/P(대출) |
III. 사례 기반 나이브 베이지안 문제 풀이
가. 지도학습 분류 결과
| 번호 | 단어 | 장르 |
|---|---|---|
| 1 | Fun, Couple, Love, Love | Comedy |
| 2 | Fast, Furious, Shoot | Action |
| 3 | Couple, Fly, Fast, Fun, Fun | Comedy |
| 4 | Furious, Shoot, Shoot, Fun | Action |
| 5 | Fly, Fast, Shoot, Love | Action |
나. 나이브 베이지안 기반 분류 결과
| 계산 과정 | 풀이 |
|---|---|
| 지도학습 분류 결과 | P(Comedy) = 2/5 = 0.4 P(Action) = 3/5 = 0.6 → 5개 문서를 통해 분류된 결과 |
| 입력 벡터 | D = Fun, Furious, Fast → 3가지 단어로 장르 선정 |
| 빈도 계산 |  |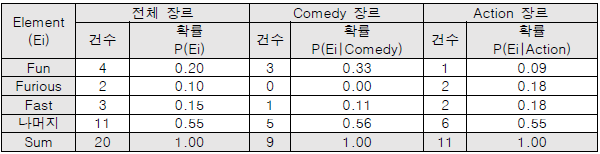
| 확률 계산 |  |
| 분류 결과 | – Action 장르일 확률이 높기 때문에 주어진 입력 벡터로 분류되는 장르는 Action으로 분류 |
- 나이브 베이지안은 미제시 요소가 입력벡터로 존재할 경우 확률이 0이되는 Zero 조건부 확률 존재
- 확률은 항상 1보다 작으므로 입력 벡터 탐색 시 비교가 어려움
IV. 나이브 베이지안의 한계점 및 보완 기법
가. 나이브 베이지안의 한계점
| 한계점 | 설명 | 극복 방안 |
|---|---|---|
| Zero 조건부 확률 | – 학습 벡터에 미제시 요소가 입력 벡터 존재 시 조건부 확률은 항상 0 | Laplace Smoothing |
| Underflow 현상 | – 확률은 항상 1보다 작으므로 조건부 확률의 값이 작아 비교가 어려움 | Log 변환 |
나. 나이브 베이지안 보완 기법
| 보완 기법 | 설명 | 특징 |
|---|---|---|
| 강화 학습 기반 재학습 | – 분류 입력 벡터를 학습 벡터로 추가하여 재학습 | 성능 저하 발생 |
| Laplace Smoothing | – 모든 Element 빈도 계산 시 1을 더하여 추출 | 조건부 확률 0 이상 |
| Log 변환 | – 각 조건부 확률에 Log e를 치환하여 적용 | 비교 용이 |
About The Author
