2018년 11월 20일
이진 탐색 트리 (Binary Search Tree)
1. 평균 탐색 속도 보장, 이진 탐색 트리의 개요
(1) 이진 탐색 트리의 개념
- 중복된 노드가 없고 왼쪽 서브 트리에는 작은 값, 오른쪽 서브 트리에는 큰 값으로 구성되는 이진 트리
(2) 이진 탐색 트리의 특징
- O(log N)의 평균 탐색 속도 보장
- 삽입/삭제 시 트리 재구성 필요
2. 이진 탐색 트리의 데이터 삽입 과정
(1) 이진 탐색 트리 데이터 삽입 알고리즘
| 단계 | 설명 |
|---|---|
| 1단계 | – 전체 트리에서 삽입하고자 하는 값 존재 탐색 |
| 2단계 | – 탐색 성공 시, 해당 값이 존재하므로 삽입 종료 |
| 3단계 | – 탐색 실패 시 부모 노드가 NULL이면 해당 노드에 값 삽입 |
| 4단계 | – 부모 노드 값과 비교하여 작으면 왼쪽, 크면 오른쪽 서브 노드로 삽입 |
- 전위/중위/후위 등 일정한 트리 순회 규칙 기반 트리 탐색 후 삽입 수행
(2) 이진 탐색 트리 데이터 삽입 과정 상세 설명
| 단계 | 삽입 과정 | 설명 |
|---|---|---|
| 1단계 | 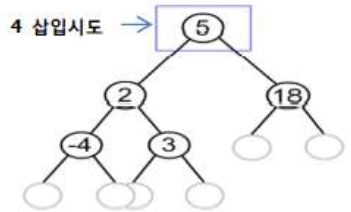 | – 삽입하고자 하는 키 값이 루트 노드의 키 값보다 작으므로 왼쪽 서브 트리 탐색 |
| 2단계 | 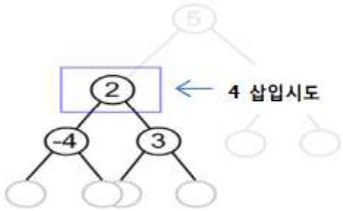 | – Level2의 왼쪽 서브 노드 키 값과 비교 – 삽입하려는 키 값이 크므로 오른쪽 서브 트리 탐색 |
| 3단계 | 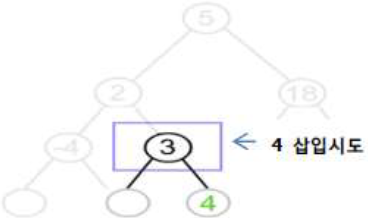 | – Level3의 오른쪽 서브 노드의 키 값과 비교 – 삽입하려는 값이 크므로 오른쪽 서브 트리 탐색 – 탐색 시도한 서브 트리가 NULL이므로 삽입 |
3. 이진 탐색 트리의 구현 사례(C언어)
| Node 자료 구조 | 삽입코드 |
|---|---|
| typedef struct Node { struct Node* Left; struct Node* Right; int Data; } Node; | void insertNode(Node** Tree, Node* newNode) { Node* tmpNode = *Tree; if (tmpNode == NULL) tmpNode = newNode; else if (tmpNode->Data > newNode->Data) insertNode(&tmpNode->Left, newNode); else if (tmpNode->Data < newNode->Data) insertNode(&tmpNode->Right, newNode); *Tree = tmpNode; } |