2018년 11월 26일
최소 신장 트리 (MST, Minimal Spanning Tree)
I. 비순환 연결 트리, 최소 신장 트리
가. 최소 신장 트리의 개념
연결 그래프의 연결된 간선 일부를 사용하여 모든 정점을 포함하여 가중치의 합이 최소가 되는 트리
나. 최소 신장 트리의 특징
| 모든 정점 포함 | – 그래프에 포함된 모든 정점을 포함 |
| 비순환 구성 | – 구성된 트리는 순환이 존재하지 않음 |
| 최소 비용 | – 모든 간선의 가중치 합을 최소화 |
II. 최소 신장 트리 개념도
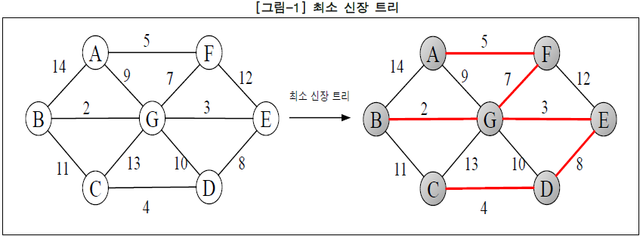
– 모든 정점 포함, 비순환, 가중치 합이 최소가 되는 신장 트리
III. 최소 신장 트리 대표 알고리즘
가. Prim 알고리즘

| 개념 | – 노드 연결 간선 가중치 합이 최소가 되도록 인접 정점을 단계적 수행하는 비순환 기법 |
|---|---|
| MST 생성 절차 | ① 임의 정점을 선택하여 최소 신장 트리의 초기 집합으로 구성 ② 앞 단계 신장 트리 집합에 인접한 정점 중 최저 비용 간선으로 연결된 정점 선택 확장 ③ n-1개의 간선이 될 때까지 ② 반복 |
| MST 생성 방법 | – 루트 노드를 기준으로 하나의 트리를 확장해 나가는 방식 |
나. Kruskal 알고리즘
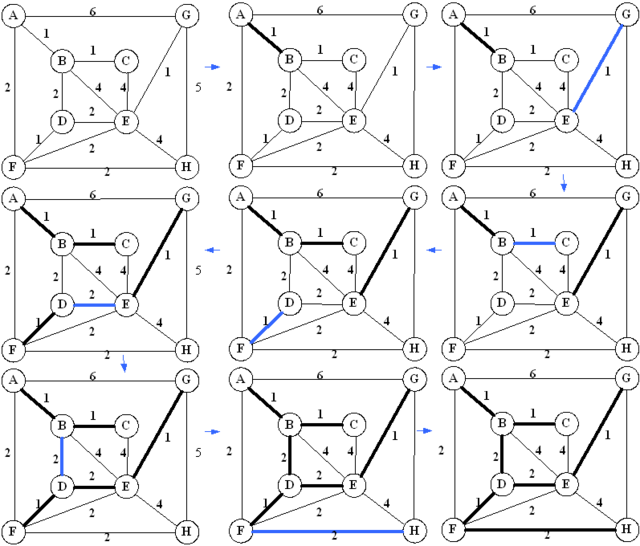
| 개념 | – 간선 비용 정렬하여 최소 비용 집합부터 선택하는 최소 비용 비순환 그래프 알고리즘 |
|---|---|
| MST 생성 절차 | ① 그래프 G의 모든 간선을 비용으로 정렬 ② 가장 작은 가중치의 간선을 하나의 집합으로 형성하고, 트리에 추가 ③ n-1개의 간선이 될 때까지 ② 반복 |
| MST 생성 방법 | – 간선의 비용을 정렬하여 최소 비용 간선부터 순차적으로 트리를 추가하여 확장하는 방식 |
다. Solin 알고리즘

| 개념 | – 단계마다 여러 개의 간선이 선택되는 방법 |
|---|---|
| MST 생성 절차 | ① 그래프의 모든 정점들이 트리를 형성 ② 각 트리에 대해 최소 비용를 갖는 간선을 선택하여 연결(순환구조는 피함) ③ n-1개의 간선이 될 때까지 ② 반복 |
| MST 생성 방법 | – 인접 간선 중 최소 비용 간선 선택, Prim유사 – 모든 간선을 비용으로 정렬, Kruskal과 유사 |
IV. 최소 신장 트리의 응용 사례
| 도로 건설 | – 도시를 모두 연결하여 도로 길이 최소화 |
| 전기 회로 | – 단자를 모두 연결하여 전선 길이 최소화 |
| 통신 | – 전화선의 길이가 최소화하여 케이블망 구축 |
| 배관 | – 파이프를 모두 연결하여 총 길이를 최소화 |
| 네트워크 | – 라우터 경로 설정, 최적의 라우팅 경로 선택 |