2022년 7월 29일
해밍 거리 (Hamming Distance)
1. 해밍 거리(Hamming Distance)의 개념
- 송/수신 데이터 오류 검출 및 오류 정정 등을 위해 두 데이터 간의 유사도를 수치화하는 함수
2. 해밍 거리 도출 메커니즘 및 오류 검출/정정 능력
(1) 해밍 거리 도출 사례 기반 메커니즘
- 같은 길이를 가진 두 부호열 또는 비트열에 대해 같은 위치에서 서로 다른 기호의 개 수(Hamming Weight)로 산출
| 해밍 거리 도출 사례 기반 메커니즘 | 사례 설명 |
|---|---|
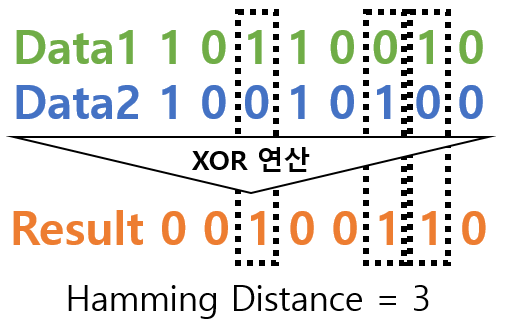 | – Data1, Data2를 XOR 한 결과(00100110)의 Hamming Weight는 3이므로, Hamming Distance는 3으로 판단 – Hamming Weight: 부호열 중 ‘0’이 아닌 부호의 개 수 |
(2) 해밍 거리를 이용한 오류 검출/정정 능력
| 구분 | 산출식 | 설명 |
|---|---|---|
| 오류 검출 능력(td) | td ≤ dmin – 1 | 검출 가능한 최대 오류의 개 수 |
| 오류 정정 능력(tc) | tc = {(dmin – 1) / 2} | 정정 가능한 최대 오류의 개 수 |
- dmin: 최소 해밍 거리(Minimum Hamming Distance), 두 개 이상의 데이터 간 해밍 거리 중 가장 작은 거리.
- 해밍 거리는 인공지능 분야의 유사도 측정을 위한 협업 필터링 등 추천시스템 Data 분석 및 네트워크 분야 전진오류수정(FEC)을 위한 해밍 코드 구현 시 활용
3. 오류 검출 및 정정을 위한 최소 해밍 거리
(1) 오류 검출을 위한 최소 해밍 거리
| 산출식 | 사례 기반 설명 |
|---|---|
| dmin = m + 1 | – 송신측이 보낸 신호 1bit{해밍 코드 2bit}: 0{00} 혹은 1{11} – 수신측에서 받을 수 있는 신호: {00, 01, 10, 11} – 수신측에서 신호 수신 시: 00 : 0 (오류 없음) 01 : 오류 (오류 검출) 10 : 오류 (오류 검출) 11 : 1 (오류 없음) |
(2) 오류 정정을 위한 최소 해밍 거리
| 산출식 | 사례 기반 설명 |
|---|---|
| dmin = 2m + 1 | – 송신측이 보낸 신호 1bit{해밍 코드 3bit}: 0{000} 혹은 1{111} – 수신측에서 받을 수 있는 신호: {000, 001, 010, 011, 100, 101, 110, 111} – 수신측에서 신호 수신 시: 000 : 0 (오류 없음) 001 : 0 (3번째 bit 0으로 정정) 010 : 0 (2번째 bit 0으로 정정) 011 : 1 (1번째 bit 1로 정정) 100 : 0 (1번째 bit 0으로 정정) 101 : 1 (2번째 bit 1로 정정) 110 : 1 (3번째 bit 1로 정정) 111 : 1 (오류 없음) |
- 수신측에서 오류 정정을 위해 7 bit의 데이터를 송신할 때 2 x 7 + 1 = 15이므로 최소 해밍 거리인 15 bit의 해밍 코드가 필요하지만, 실제 해밍 코드 기반 오류 검출/정정 시 최소한의 Parity bit를 이용하여 11bit의 해밍 코드 만으로도 오류 정정 가능
4. 해밍 코드 도출 및 오류 검출/정정 과정 사례
(1) Parity bit 기반 해밍 코드 도출
- 전송 데이터: 1001101, 짝수 패리티 비트로 추가
| 과정 | 설명 | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 패리티 비트 계산 | 2p – 1 ≥ d + p (p: 패리티 자리 수, d: 데이터 자리 수) d = 7이므로, 2p – 1 ≥ 7 + p ∴ p = 4, 패리티 자리 수는 4 | ||||||||||||||||||||||
| 데이터 배치 | 2n 자리를 제외한 자리에 데이터 배치
| ||||||||||||||||||||||
| 짝수 패리티 기반 체크 비트 도출 | R1 = 1 (1, 3, 5, 7, 9, 11 자리의 1의 개수가 짝수 유지)
(1, 0, 1, 0, 1, R1) → 짝수, ∴ R1 = 1 | ||||||||||||||||||||||
| 패리티 비트 배치한 해밍코드 |
|
(2) 해밍코드 오류 검출 과정
| 과정 | 설명 | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 수신 데이터 배치 |
| ||||||||||||||||||||||
| 체크 비트 확인 | R = 1 (1, 3, 5, 7, 9, 11번째 값과 짝수 패리티 유지)
∴ 1이 3개, R1 = 1 | ||||||||||||||||||||||
| 오류 자리 확인 | 0111 → 7번째 자리 비트 오류 |
- 패리티 비트의 결과값이 오류 비트의 위치
(3) 해밍 코드 오류 정정 과정
| 과정 | 설명 | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 오류 자리 | 0111 → 7번째 자리 비트 오류 | ||||||||||||||||||||||
| 7번째 자리 수정 | 7번째 자리 “0”을 그 보수인 “1”로 변경
| ||||||||||||||||||||||
| 오류 수정 결과 |
∴ 정상 비트는 10011100101 |