2018년 11월 23일
회귀분석 (Regression Analysis)
1. 독립변수와 종속변수 간 상관관계, 회귀분석
(1) 회귀분석의 개념
- 관찰된 변수 집합에서 독립변수와 종속변수 간 상관관계를 함수식으로 표현 및 검증하는 분석기법
(2) 회귀분석 모형의 가정
| 구분 | 구성요소 |
|---|---|
| 변수 선형성 | – 독립변수와 종속변수 관계는 선형적 |
| 오차 정규성 | – 오차의 기대값은 ‘0’이며, 정규분포 |
| 오차 독립성 | – 오차들은 서로 독립적 |
2. 회귀분석 모델/구성요소 및 분석 유형
(1) 회귀분석 모델/구성요소
| 모델 | 구성요소 | 설명 |
|---|---|---|
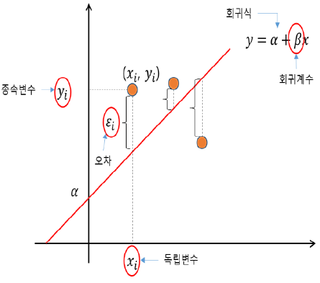 | 독립변수 | 입력값, 원인 변수 |
| 종속변수 | 독립변수 의한 효과 | |
| 회귀계수 | 변화량, 기울기 | |
| 최소자승법 | 각점 거리 최소선 | |
| 회귀방정식 | 회귀선 수학적 함수 |
- 산포된 점들이 회귀선에 수직으로 이르는 값들의 최소가 되는 회귀 계수 산출이 핵심
(2) 회귀분석의 다양한 유형
| 구분 | 유형 | 설명 |
|---|---|---|
| 독립변수 수 기반 | 단순 회귀 분석 | – y=ax+b, 독립변수 1개 |
| 다중 회귀 분석 | – y=ax1+…+cxn,독립변수다수 | |
| 종속변수 수 기반 | 일변량 회귀 분석 | – 분석 모형, 종속변수 1개 |
| 다변량 회귀 분석 | – 분석 예측, 종속변수 다수 | |
| 종속변수 형태기반 | 선형 회귀 분석 | – 직각거리 최소화 회귀분석 |
| 로지스틱 회귀 분석 | – 다항, 분화 로지스틱 분류 |
- 회귀분석의 가정 상 변수들은 서로 독립적이어야 하나, 상관관계 발생 시 공선성 확인 및 해결 필요
3. 회귀분석에서 나타나는 공선성 문제의 해결 방안
| 구분 | 해결 방안 | 설명 |
|---|---|---|
| 공선성 유발변수 확인/제거 측면 | 공선성 유발 변수 확인 | – R2값 최대 변수 유발 판정 – t-검정통계량 귀무가설 기각시 |
| 공선성 유발 변수 제거 | – 작은 상관계수의 설명변수제거 – β계수, 탄력성(β^i (Xi /Y)) 이용 | |
| 모형 보완 및 변형 측면 | 모형 보완 | – 추가적 표본관측치 확보/활용 – 기존 평균값과 상이한 값 포함 |
| 모형 변형 | – 일차분차식, 비율식 사용 – ∆Yi=α+β1∆X1i+β2∆X2i+εi |
- 회귀분석의 추정 성능확보와 공선성 문제 해결 위해 t-분포, f-분포, 유의수준과 p-value 등 검증 필요