2019년 1월 25일
DBSCAN
I. 밀도기반 군집화 기법, DBSCAN
가. DBSCAN 의 개념
- 핵심 벡터로부터 ε 반경 내 접근 가능한 모든 데이터 벡터들의 집합(군집)을 생성하는 기법
- DBSCAN : Density-Based Spatial Clustering of Application with Noise
나. DBSCAN 주요 개념
| ε (epsilon) | – 주어진 개체 들의 반경 |
| minPts | – ε 반경 내 군집 위해 필요한 객체 수 |
II. 군집 생성 요소 및 절차
가. 군집 생성 요소
| 구성 요소 | 설명 |
|---|---|
| 이웃 벡터 | – 한 벡터로부터 ε 반경 내 위치한 다른 데이터 벡터 |
| 핵심 벡터 (Core Point) | – n개 이상의 이웃벡터를 갖는 데이터 벡터 |
| 직접 접근 가능 | – directly density-reachable – 핵심 벡터 p와 p의 이웃벡터 q에 대해 q는 p에 대해 직접 접근 가능 (p→q) |
| 접근 가능 | – density-reachable {p=p1→p2, … , →q} – 벡터 p와 q에 대해 직접 접근 가능한 데이터 벡터 배열 |
| 연결된 | – density-connected – 벡터 p와 q에 대해 접근 가능한 벡터 o가 존재(o→p, o→q), p와 q는 서로 연결(p↔q) |
| 군집 (Cluster) | – 한 핵심벡터 p에 대해 접근 가능한 모든 데이터 벡터들의 집합, 군집 내 벡터는 연결 |
| 노이즈 (Noise) | – 어떠한 군집에도 속하지 않는 데이터 |
나. 군집 생성 절차
| 절차 | 개념도 | 설명 |
|---|---|---|
| 기본 상태 |  | – ε (epsilon) : 주어진 객체들의 반경 – minPts : 군집 최소수 – ε 반경 내 minPts개가 존재해야 군집 판단 |
| 군집 생성 | 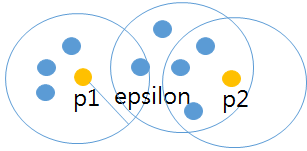 | – 임의 점 p1, p2 등에서 ε 반경 내 minPts 만족 시 군집 |
| Noise 분류 |  | – 임의 점 p1 에서 ε 반경 내 p2 미 존재 시 Noise로 분류 |
| 군집 완성 | 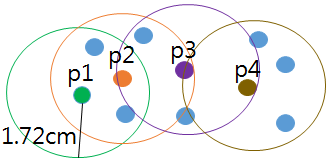 | – 각 점에서 ε 반경 내 minPts 충족하는 객체집합(군집) 완성 |
III. DBSCAN의 장/단점
| 장점 | 단점 |
|---|---|
| – 군집개수 정의 필요 없음 – 임의 모양의 군집 생성 – 잡음(Noise) 개념 존재 – 2개의 매개변수만 필요 | – 유클리디안 거리 이용하여 ε 산출이 어려움 – 다차원 및 고밀도 데이터의 군집화 어려움 |