2018년 11월 23일
다익스트라 알고리즘 (Dijkstra’s Algorithm)
I. 최단 거리 계산, 다익스트라 알고리즘
가. 다익스트라 알고리즘의 개념
정점에서부터 다른 모든 정점들까지 증가하는 거리 순 최단 경로를 찾는 알고리즘
나. 다익스트라 알고리즘 절차
| 단계 | 절차 | 세부 설명 |
|---|---|---|
| ① | – 각 노드 거리 설정 | – 시작 노드 외 각 노드의 거리에 무한대(∞) 적용 |
| ② | – 거리 측정 | – 시작노드로부터 각 노드까지 계산 |
| ③ | – 최소거리선택 | – 시작 노드부터 도착 노드까지 최소비용 간선의 노드 연결 |
II. 다익스트라 알고리즘 사례
| 단계 | 구성도 | 설명 |
|---|---|---|
| 1단계 | 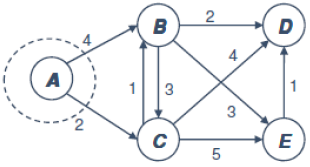 – 출발지(A) 외 모든 정점 경로 ∞ | A: 0 B: ∞ C: ∞ D: ∞ E: ∞ |
| 2단계 | 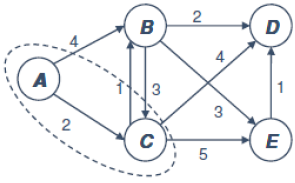 – A부터 연결된 최소 가중치 선택 | A: 0 B: ∞ C: 2 D: ∞ E: ∞ |
| 3단계 | 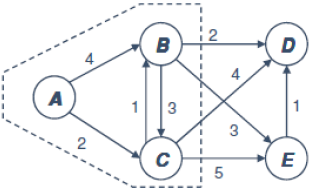 – A부터 연결된 최소 가중치 선택 | A: 0 B: 3 C: 2 D: ∞ E: ∞ |
| 4단계 | 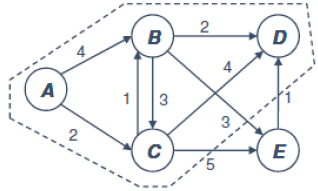 – A부터 연결된 최소 가중치 선택 | A: 0 B: 3 C: 2 D: 5 E: ∞ |
| 5단계 | 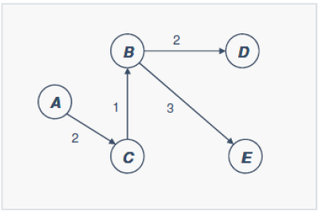 – 모든 노드 연결 시 연결 종료 | A: 0 B: 3 C: 2 D: 5 E: 6 |
III. 다익스트라 알고리즘 의사코드
| function Dijkstra(G, w, s) for each vertex v in V[G] // 초기화 d[v] := infinity previous[v] := undefined d[s] := 0 S := empty set Q := set of all vertices While Q is not an empty set u := Extract_Min(Q) // 시작점부터 정점까지 경로합 중 최소값 선택 S := S union{u} for each v with edge (u, v) defined if d[v] > d[u] + w(u, v) d[v] := d[u] + w(u, v) previous[v] := u // 경로 추적 시 사용 |
About The Author
