2024년 12월 9일
의사결정나무 (Decision Tree)
1. 지도 학습 모델, 의사결정나무 (Decision Tree)의 개념
| 개념도 | 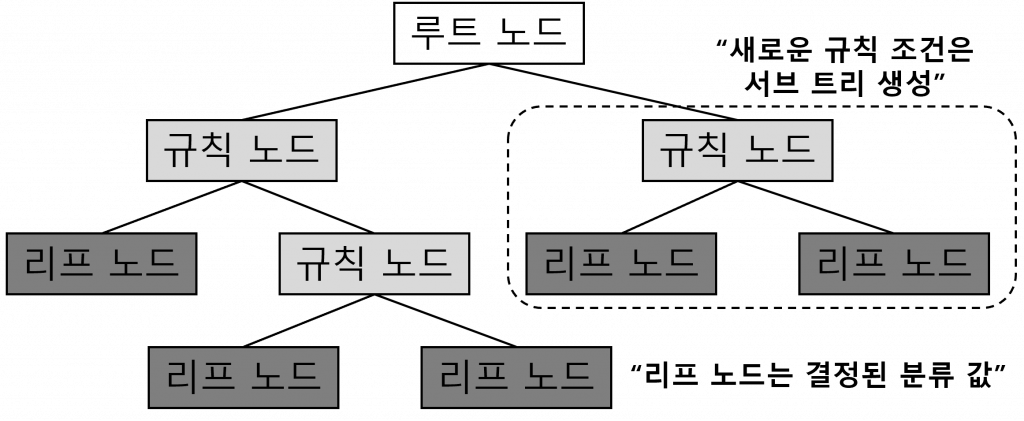 |
|---|---|
| 개념 | 빅데이터 및 인공지능 분석을 위해 의사결정 규칙을 나무 구조로 도표화하여 분류와 예측을 수행하는 분석 기법 |
- 의사결정 나무 (의사결정 트리)는 두 개 이상의 변수가 결합하여 목표 변수에 어떻게 영향을 주는지 쉽게 알 수 있으며, 트리 구조로 표현되기 때문에 모형을 쉽게 이해
2. 의사결정나무 기반 분석 절차 및 구성요소
(1) 의사결정나무 기반 분석 절차
 |
| 분석 절차 | 주요 기법 | 세부 활동 |
|---|---|---|
| 의사결정나무 형성 | – 재귀적 분할 알고리즘 – 불순도(Impurity) 지수 | – 분석 목적을 정의하고, 목적에 따라 적절한 분리규칙 (Splitting rule)을 찾아 트리를 전개하는 과정 – 적절한 정지 규칙(Stopping rule)을 만족하면 성장 중단 |
| 가지치기 | – 사전 가지치기 (Pre-Pruning) – 사후 가지치기 (Post-Pruning) | – 결정나무 크기가 너무 큰 모형은 과적합, 너무 작은 나무 모형은 과소 적합될 수 있는 문제를 해결 – 과적합 발생하는 것을 방지하기 위해 불필요한 가지들을 제거 |
| 타당성 평가 | – 교차 검증 (Cross-Validation) | – 이익 도표(Gains Chart)나 위험 도표(Risk Chart) 또는 검증용 자료(Test Data)에 의한 교차 검증(Cross-Validation) 기반 의사결정나무 평가 |
| 해석 및 예측 | – 범주형 데이터 – 수치형 데이터 | – 완성된 의사결정나무 모형을 해석하고, 분류 및 예측 모형을 설정하여 데이터 분류 및 예측에 활용 |
(2) 의사결정나무의 구성요소
| 구분 | 구성요소 | 역할 |
|---|---|---|
| 노드 | 뿌리 마디 (Root Node) | 나무가 시작되는 마디로 전체 자료를 포함 |
| 중간 마디 (Internal Node) | 부모와 자식 마디를 모두 가진 마디 | |
| 끝 마디 (Terminal Node) | 자식 노드가 없는 마디 | |
| 부모 마디 (Parent Node) | 주어진 노드의 상위 마디 | |
| 자식 마디 (Child Node) | 주어진 노드의 하위 마디 | |
| 속성 | 가지 (Branch) | 하나의 마디부터 끝 마디까지 연결된 마디들 |
| 깊이 (Depth) | 가지를 이루는 마디의 개수 |
- 의사 결정 나무의 깊이(depth)가 깊어 과적합(overfitting)이 발생하는 것을 방지하기 위해 가지치기(Pruning)를 이용하여 불필요 가지들을 제거
3. 의사결정나무의 분류 및 평가 지표
(1) 의사결정나무의 분류
| 분류 나무 (Classification Tree) | 회귀 나무 (Regression Tree) |
|---|---|
| – 출력 변수가 범주형 – 목표 변수가 이산형인 경우 – 지니 (Gini), 엔트로피 (entropy) 지수 등 | – 출력 변수가 연속형 – Top-Down의 Greedy(탐욕) 방식 탐색 – 오차제곱합(MSE) 사용 |
(2) 의사결정나무의 평가 지표
| 구분 | 평가 지표 | 평가 방법 |
|---|---|---|
| 분류 나무 (Classification Tree) | 지니 지수 (Gini Index) | – K개 클래스에 걸친 총 분산의 측도 산출 – 노드 순도라고 부르며, 작은 값은 노드가 단일 클래스로부터의 관측치들이 주로 포함 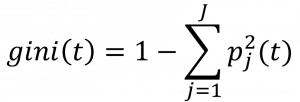 |
| 엔트로피 (Entropy) | – 무질서한 정도를 나타내는 지표 – 엔트로피가 최소화 되도록 분석 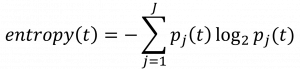 | |
| 회귀 나무 (Regression Tree) | 오차제곱합 | – MSE(Mean Squared Error) – 실제값과 예측값의 차이를 제곱 후 더해주는 과정 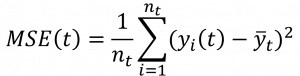 |
- 의사 결정 트리는 이해하기 쉽고 영향도 파악이 용이하며, 계산복잡성 대비 높은 예측성능으로 분류와 회귀 모두 분석 가능하지만 최적해를 보장하지 못하고 비연속성 분류, 결정 경계가 데이터 축에 수직인 데이터에만 최적화 가능한 단점 존재
- 과적합(overfitting)된 학습으로 예측 및 분류 성능이 떨어질 수 있는 의사 결정 나무의 한계점은 일반적으로 앙상블(Ensemble) 기법을 통해서 해결가능
4. 의사결정나무 과적합 해결, 랜덤 포레스트(Random Forest)
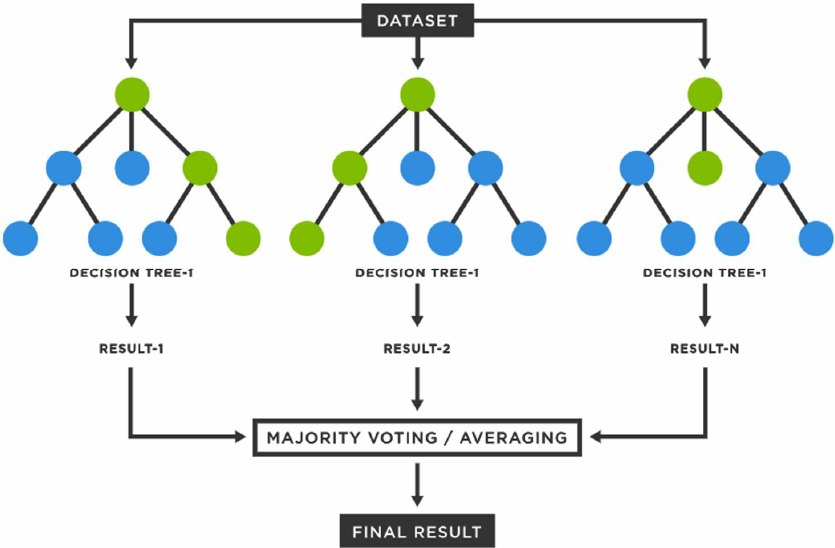 |
- 랜덤 포레스트(Random Forest)를 통해 다수의 약한 분류기(Weak Classifier)들을 결합하여 하나의 강한 분류기(Strong Classifier) 생성 가능
[참고]
- 나종화, KOCW 데이터마이닝 및 실험(충북대학교, 2017)
- 빅데이터&머신러닝랩, 의사결정나무모형(동국대학교)