2023년 12월 19일
트리 순회 (Tree Traversal)
1. 트리 순회(Tree Traversal)의 개요
(1) 트리 순회의 개념
- 트리 구조에서 트리의 모든 노드를 정확히 한 번씩 체계적으로 방문하는 과정
(2) 트리 순회의 특징
| 그래프 탐색 | 노드 간 연결된 그래프를 탐색하는 과정 |
|---|---|
| 재귀 순환 | 각 서브 트리를 재귀적인 방법으로 순회 |
| 시간 복잡도 | 이진 트리 평균 시간 복잡도: O(log n) |
- 트리 순회는 트리 구조를 통해 효율적으로 원하는 데이터에 접근하는 방법을 제공하고 이진 트리를 포함하여 모든 트리에 대해 재귀함수를 통해 쉽게 구현 가능
- 전체 노드 접근 시 큐, 스택, 연결 리스트 등은 순차적으로 접근하지만 트리의 경우 전위/중위/후위 순회 방식을 통해 접근
2. 트리 순회 방식 별 접근 순서 및 사례
| 방식 | 접근 순서 | 사례 / 활용 |
|---|---|---|
| 전위 순회 (Preorder Traversal) | 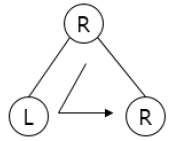 – 접근 순서: Root → Left →Right – 접근 순서: Root → Left →Right |  – 트리 복사에 활용 – 트리 복사에 활용 |
| 중위 순회 (Inorder Traversal) | 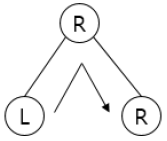 – 접근 순서: Left → Root →Right – 접근 순서: Left → Root →Right | 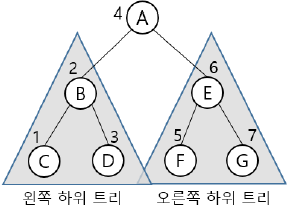 – 수식 트리, 오름/내림차순 – 수식 트리, 오름/내림차순 |
| 후위 순회 (Postorder Traversal) | 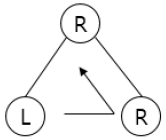 – 접근 순서: Left → Right →Root – 접근 순서: Left → Right →Root | 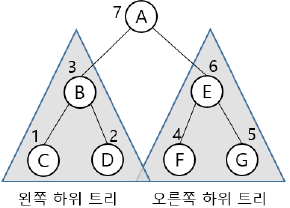 – 트리 삭제에 활용 – 트리 삭제에 활용 |
- 전위순회 방식은 깊이우선순회(DFT, Depth First Traversal)라고도 하며, 중위순회 방식은 이진탐색트리에서 오름차순 또는 내림차순으로 값을 가져올 때 사용하고, 후위순회 방식은 부모 노드 삭제 전 자식 노드를 삭제하여 트리를 삭제하는데 주로 사용
3. 트리 순회 방식 별 소스 코드
| 구조체 | typedef struct { int data; struct TreeNode *left; struct TreeNode *right; } TreeNode; |
|---|---|
| 전위 순회 | void preOrder(TreeNode *node) { if(node == NULL) return; printf(“%d “, node->data); // root 방문 preOrder(node->left); // 왼쪽 sub tree 방문 preOrder(node->right); // 오른쪽 sub tree 방문 } |
| 중위 순회 | void inOrder(TreeNode *node) { if(node == NULL) return; inOrder(node->left); // 왼쪽 sub tree 방문 printf(“%d “, node->data); // root 방문 inOrder(node->right); // 오른쪽 sub tree 방문 } |
| 후위 순회 | void postOrder(TreeNode *node) { if(node == NULL) return; postOrder(node->left); // 왼쪽 sub tree 방문 postOrder(node->right); // 오른쪽 sub tree 방문 printf(“%d “, node->data); // root 방문 } |
[참고]
- 한빛미디어, 뇌를 자극하는 알고리즘